Главная - Статьи - Понятие о генеральной совокупности и выборке. Описательная статистика...

Е. О. Юдин

Понятие о генеральной совокупности и выборке. Описательная статистика, как метод разведочного анализа данных.

Основная цель использования методов математической статистики - изучение свойств неизмеримо большой группы объектов на основании анализа свойств относительно небольшой их совокупности.

При этом все существующее в природе множество интересующих нас объектов называется генеральной совокупностью, а относительно небольшое их множество, отобранное нами для изучения - выборочной совокупностью, или выборкой.

Применительно к морфометрии это можно продемонстрировать на следующем примере: допустим мы хотим изучить изменчивость показателя ядерно-цитоплазменного отношения клеток печени (гепатоцитов) мыши на различных этапах жизни животного, т.е. в онтогенетическом аспекте. Все существующие в природе мыши различного возраста будут являться членами генеральной совокупности. Но изучить всех мышей физически невозможно. Поэтому для того, чтобы получить представление об изменчивости интересующего нас параметра мы отбираем из их общего количества (т.е. из генеральной совокупности) относительно небольшую группу мышей (выборку), гепатоциты которых и подвергаются изучению. Выводы, полученные нами при изучении выборки мы распространяем (генерализуем) на всех мышей, т.е. на всю генеральную совокупность.

Для того, чтобы выводы, сделанные на основании изучения выборки были максимально приближены к действительным свойствам генеральной совокупности выборка по своей структуре должна быть пропорциональна всей генеральной совокупности, или как говорят матстатистики репрезентативна ей. Как правило для формирования правильной репрезентативной выборки используется метод случайного отбора.

Строго говоря выборка представляет собой ряд последовательных измерений какого-либо параметра (в вышеприведенном примере - ядерно-цитоплазменного отношения гепатоцитов мыши). Параметр (свойство), который мы измеряем при исследовании называется переменной, т.к. его значения как правило являются неодинаковыми и образуют ряд случайных значений. Для того, чтобы математически описать изменчивость случайных значений и были разработаны методы описательной статистики.

Описательная статистика включает в себя несколько базовых показателей, которые можно разделить на три основных группы: показатели положения и показатели разброса. В целом описательные статистики характеризуют положение выборки относительно числовой прямой, а также форму ее распределения. Понятие о распределении будет введено в следующей статье, пока же остановимся на детальной характеристике описательных статистик.

Показатели положения.

К таковым относятся: среднее арифметическое, медиана, мода. Эти описательные статистики характеризуют положение выборки относительно числовой прямой.

Среднее арифметическое выборки (англ. mean) это наверное один из наиболее употребительных статистических показателей. Среднее арифметическое характеризует положение центра выборки на числовой прямой и является мерой математического ожидания переменной.

Медианой (англ. median) называется значение исследуемого признака, справа и слева от которого находится одинаковое число упорядоченных элементов выборки. Если объем выборки – четное число, то медианой является среднее арифметическое двух центральных членов. Другими словами медиана разбивает выборку на две равные части. Также, как и среднее арифметическое, медиана дает общее представление о том, где находится центр выборки. В некоторых случаях медиана более удобна, чем среднее. Определение медианы было впервые использовано Гальтоном в 1882 г.

Мода (англ. mode) представляет собой наиболее часто встречающееся значение переменной (иными словами, наиболее «модное» значение переменной). Сложность состоит в том, что редкая выборка имеет единственную моду. Если в выборке несколько мод, то говорят, что она мультимодальна или многомодальна (имеет два или более «пика»). Таким образом можно сказать, что мода характеризует не только положение выборки, но отчасти и форму ее распределения.

Показатели разброса.

К показателям разброса относятся: минимум и максимум выборки и разность между ними (размах выборки), дисперсия, среднее квадратическое отклонение (стандартное отклонение). Рассмотрим эти показатели подробнее.

Минимум и максимум выборки - это соответственно наименьшее и наибольшее значение изучаемой переменной. Разность между максимумом и минимумо называется размахом выборки. Все данные выборки расположены в промежутке между минимумом и максимумом. Эти показатели как бы очерчивают границы выборки.

Дисперсия выборки (англ. variance) и среднее квадратическое отклонение выборки (англ. standard deviation) являют собой меру изменчивости переменной и характеризуют степень разброса данных вокруг центра. При этом среднее квадратическое отклонение является более удобным показателем в силу того, что имеет ту же размерность, что и собственно исследуемые данные.

Поэтому показатель среднего квадратического отклонения используется наряду со значением среднего арифметического выборки для короткого описания результатов анализа данных.

Кстати в медико-биологических исследованиях часто встречаются записи результатов вида "M±m". Это может быть истолковано неоднозначно, т.к. в качестве "М большого" всегда используется среднее выборки, а вот в качестве "М малого" может выступать как среднее квадтратическое отклонение, так и стандартная ошибка среднего. Поэтому при использовании записей подобного вида всегда уточняйте какие показатели были использованы.

Показатель асимметрии (англ. skewness) используется для того, чтобы охарактериховать степень симметричности распределения данных вокруг центра. Асимметрия может принимать как отрицательные, так и положительные значения. Положительное значение данного параметра указывает на то, что данные смещены влево от центра, отрицательное - вправо. Таким образом знак показателя асимметрии указывает на направление смещения данных, тогда как величина - на степень этого смещения. Асимметрия равная нулю говорит о том, что данные симметрично сконцентрированы вокруг центра.

Коэффициент эксцесса (англ. kurtosis) является характеристикой того, насколько кучно основная масса данных группируется около центра.

Каково же прикладное значение описательных статистик, применительно к морфометрическим исследованиям?

Описательные статистики дают нам возможность оценить характер распределения данных в изучаемой выборке. На основании этой оценки мы можем принять решение о том какие критерии надлежит использовать в дальнейшей работе - например при сравнении выборок.Описательные статистики являются основой построения статистических графиков и диаграмм - например диаграмм размаха, т.е. являются предварительным этапом в проведении визуального анализа данных. Таким образом, можно отнести их к категории разведочных методов анализа данных.

Рассмотрим методику расчета описательных статистик в программе Statistica 6.0:

Первым делом нам необходимо ввести данные выборки в чистый файл. Предположим это все те же данные измерения ядерно-цитоплазменного отношения гепатоцитов мыши (см. рис. 1):

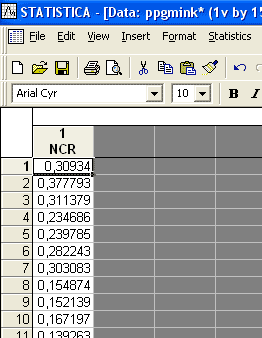
Рис. 1 Подготовленная выборка.

Выберем пункт меню Statistics - Basic Statistics/Tables (см. рис. 2):

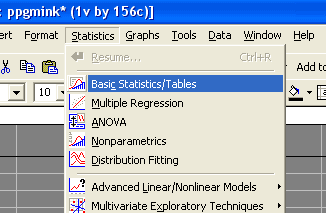
Рис. 2 Пункт меню Basic Statistics/Tables.

В открывшемся модальном окне Basic Statistics and Tables необходимо выделить пункт Descriptive Statistics и нажать кнопку ОК:

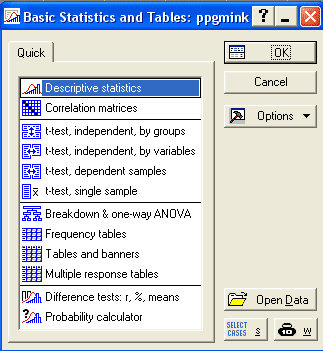
Рис. 3 Окно Basic Statistics and Tables.

В результате этого откроется окно Descriptive Statistics. Нажмите кнопку Variables и в появившемся окне Select the variables for the analyses выберите имя той переменной, для которой необходимо расчитать описательные статистики и нажмите ОК. После этого перейдите на закладку Advanced и поставьте галочки напротив тех статистик, которые необходимо расчитать (см. рис. 4):

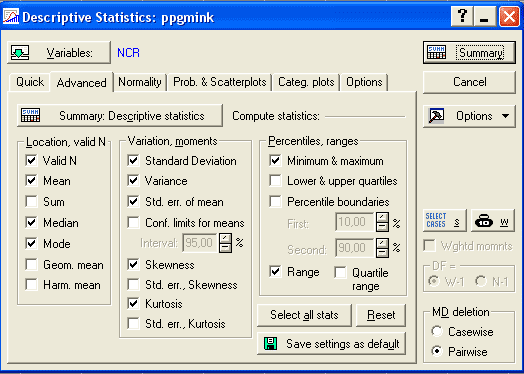
Рис. 4 Окно Descriptive Statistics с настроенными для анализа параметрами.

Теперь осталось только нажать кнопку Summary и программа откроет новую рабочую книгу с результатами расчетов.

Наверх